本篇博客摘录并翻译一篇论文（未完待续。。。）

3 有效训练

3.1 大批次训练

线性缩放学习率

在使用小批次进行随机数据的训练，增加数据批次没有改变随机梯度的期望而减少了方差。换一句话说，一个大批次大小减少梯度的噪音。因此我们可以提高学习率，以沿梯度方向的相反方向获得更大的改进。特别，如果我们遵循ResNet原论文中的对于批次大小为256时，初始学习率设置成0.1。然后，当改变一个更大的批次大小为b，我们将增加初始学习率为0.1×b/256.

学习率预热

在训练的开始，所有的参数通常是随机值，因此离最终的解决方案很远。使用过大的学习率可能会导致数值不稳定。在热身启发式中，我们在开始时使用一个小的学习速率，然后在训练过程稳定时切换回初始的学习速率。Goyalet al.[7]提出了一种渐进热身策略，将学习率从0线性增加到初始学习率。换句话说，假设我们将使用前m个批次（例如5个数据周期）进行预热，并且初始学习率为η，那么在第i批次中，1≤i≤m，我们将学习率设为iη\m。

Zero gamma

ResNet结构：一个ResNet网络由多个残差块组成，每个残差块由几个卷积层组成。给定输入x，假设block(x)是block的最后一层的输出，这个残差块将输出x + block(x)。注意，block的最后一层可以是批处理标准化(BN)层。

Batch Normalization：BN层首先标准化其输入，用\(\check{x} \)表示，然后执行一个尺度变换：\({\gamma \check{x} + \beta} \)。γ和β都是可学习的参数，其元素分别初始化为1s和0s。

zero \(\gamma \)技巧：我们对位于残差块末尾的所有BN层初始化γ= 0。 结果：所有残差块仅返回其输入，模拟网络在初始阶段具有较少的层数，更容易训练。

没有bias衰减

权重衰减（weight decay）：权值衰减通常应用于所有可学习的参数，包括权重和偏差。这相当于对所有参数应用L2正则化，使它们的值趋近于0。

改进：Jia等人指出的只对权重应用正则化，来避免过拟合。

技巧：将权重衰减应用于卷积层和完全连接层中的权重，对偏差不进行衰减。其他参数，包括BN层中的biases以及γ和β，均未调整。

大批次的使用情况：（Large batch training ofconvolutional networks with layer-wise adaptive rate scaling）论文提出分层的自适应学习率，据报告对于超大批量（超过16K）有效。将自身限于能够进行单机训练的情况下，每批不超过2K的批次通常会带来良好的系统效率。

3.2 低精度训练（数值精度类型、数值位数）

如何加快训练速度：神经网络通常采用32位浮点(FP32)精度进行训练。也就是说，所有的数字都以FP32格式存储，算术运算的输入和输出也是FP32数字。NvidiaV100在FP32中提供14 TFLOPS，但在FP16中提供100 TFLOPS。在V100上从FP32切换到FP16后，整体训练速度提高了2到3倍。（这里根据自己实验设备而定。）

存在的问题：尽管性能有所提高，但降低的精度会缩小范围，使结果更可能超出范围，进而干扰训练进度。

解决方案：（1）Micikeviciusetal建议在FP16中存储所有参数和激活，并使用FP16计算梯度。同时，FP32中的所有参数都有一个副本，用于参数更新。（2）将标量与损失（loss）相乘以更好地将梯度范围对齐到FP16。

3.3 实验结果

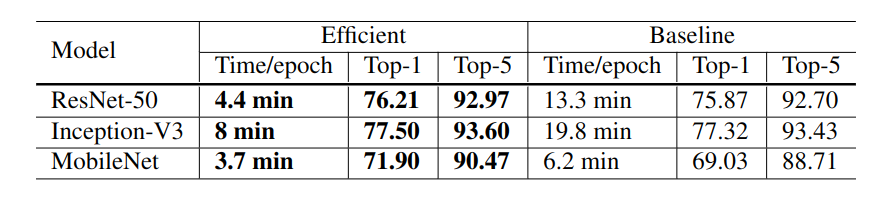
• 训练时间减少：与批量大小为256和FP32的基线相比，使用更大的1024批量大小和FP16可以将ResNet-50的训练时间从每个epoch 13.3分钟减少到4.4分钟。

• 叠加训练技巧提高精度：通过堆叠所有启发式方法进行大批量训练，与基线模型相比，使用1024批大小和FP16训练的模型甚至稍微提高了0.5％的top-1准确性。

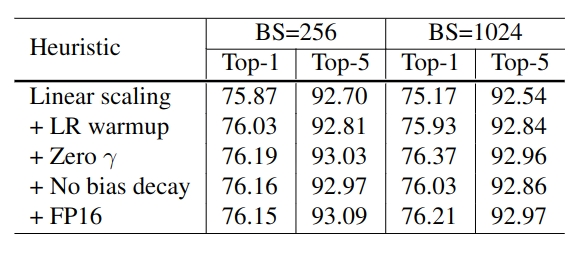
• 实验结果：表4中显示了所有启发式方法的消融研究，仅通过线性缩放学习率将批次大小从256增加到1024会导致top-1准确性降低0.9％，同时堆叠其余三个启发式方法可以弥补这一差距。在训练结束时从FP32切换到FP16不会影响准确性。

4 模型调整

4.1 ResNet结构

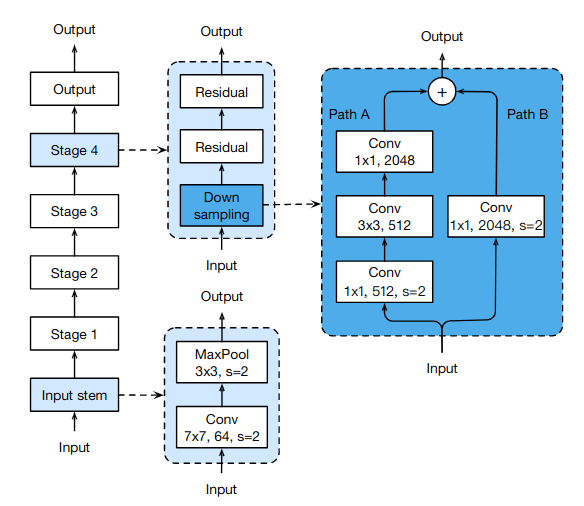
ResNet网络结构：（如图1所示），ResNet网络由输入主干，四个后续阶段和最终输出层组成。
（1）输入主干具有步长为2，输出通道为64，卷积核为7×7的卷积层，紧接着应用步长为2，核为3×3的池化层。输入主干将输入宽度和高度减少4倍，并将其通道大小增加到64。

（2）从阶段2开始，每个阶段都从一个降采样块（down sampling block）开始，然后是几个残差块（residual block）。在下采样块中，有路径A和路径B。

• 路径A有三个卷积层，其卷积核大小分别为1×1,3×3和1×1。第一个卷积的步长为2，可将输入宽度和高度减半；最后一个卷积的输出通道是前两个卷积的输出通道的4倍，这称为瓶颈结构（bottleneck block）。
• 路径B使用步长为2的1×1卷积将输入形状转换为路径A的输出形状，因此可以将两条路径的输出求和以获得下采样块的输出。

（3）残差块类似于下采样块，除了仅使用步长为1的卷积。

（4）可以在每个阶段改变残差块的数量，得到不同的ResNet模型。如ResNet18,ResNet50,ResNet152。

4.2. ResNet调整

ResNet-B，ResNet-C是已经提出的调整。论文提出的调整方案是ResNet-D

ResNet-B

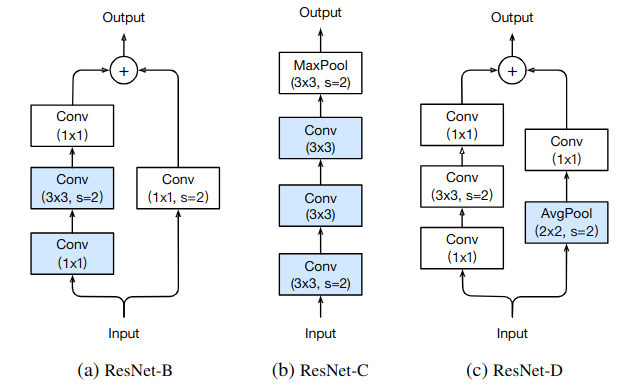
原因：它改变了ResNe的下采样块。实验观察到，路径A中的卷积忽略了输入特征图的四分之三，因为它使用的卷积核大小为1×1，步长为2。

改进：如图2a所示，ResNet-B改变路径A中前两个卷积的步长大小，所以没有信息被忽略。因为第二层卷积的卷积核大小为3×3，因此路径A的输出形状保持不变。

ResNet-C

出处：此调整最初是在Inception-v2中提出的，可以在其他模型的实现中找到，例如SENet [12]，PSPNet [31]，DeepLabV3 [1]和ShuffleNetV2 [21]。

原因：观察发现，卷积的计算成本是核宽度或高度的平方。一个7×7卷积比3×3卷积贵5.4倍。

改进：图2b所示。此调整将输入主干的7×7卷积替换为三个保守的3×3卷积，其中第一个和第二个卷积的输出通道为32，步长为2，而最后一个卷积使用64输出通道。

ResNet-D

原因（创新点）：受ResNet-B的启发，我们注意到下采样块路径B中的1×1卷积也忽略了3/4个输入特征图，我们想对其进行修改，因此不会忽略任何信息。

改进：根据经验，我们发现在卷积之前添加一个步长为2的2×2平均池化层（卷积层的步长更改为1）在实践中效果很好，并且对计算成本的影响很小。

4.3. 实验结果

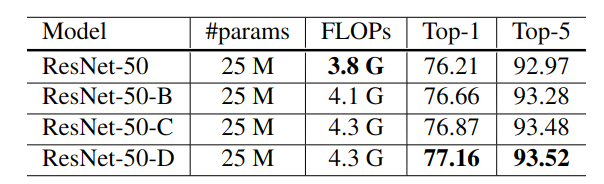
实验方案：使用第3节中描述的三种调整和设置来评估ResNet-50，即批量大小为1024，精度为FP16。结果如表5所示。

实验结果：
（1）与ResNet-50对比，ResNet-B在下采样块的路径A中可以接收到更多信息，其验证准确性提高了约0.5％。
（2）将7×7卷积替换为三个3×3卷积可进一步提高0.2％。在下采样块的路径B中可获的更多信息，可将验证准确度再提高0.3％。

结论：ResNet-50-D将ResNet-50提升了1％。

计算成本对比：四个模型具有相同的模型大小。ResNet-D具有最大的计算成本，但就浮点运算而言，它与ResNet-50的差异在15%以内。实际上，我们观察到，与ResNet-50相比，ResNet-50-D在训练吞吐量方面仅慢3%。

5 训练改进

在本节中，我们将描述四个训练改进，来进一步提高模型的准确性。

5.1. 余弦学习率衰减（Cosine learning rate decay）

来源： Loshchilov（论文：SGDR: stochastic gradient de-scent with restarts）提出一个余弦退火策略。

cosine decay：一个简化的版本是根据余弦函数将学习率从初始值降低到0。假设批次总数为T（忽略预热阶段），则在批次t处，学习率\(\eta_t\)计算为：\({\eta_t = \frac{1}{2} (1 + cos(\frac{t\pi}{T}))\eta }\)。其中\(\eta \)是初始学习率。

cosine decay 和 step decay的对比（图3a）：

• cosine decay：余弦衰减在开始时缓慢降低学习速度，然后在中间时几乎呈线性下降，在结束时再次减慢。
• 与step decay相比：余弦衰减从一开始就对学习进行衰减，但在step decay使学习速率降低10倍之前，余弦衰减仍然很大，这可能会提高训练的进度。

5.2. 标签平滑（Label Smoothing）

标签的常用使用过程

• 标签预测置信度分数->softmax预测概率：图像分类网络的最后一层通常是一个全连通层，隐藏的大小等于标签的数量，用K表示，用来输出预测的置信度分数。给定一张图像，用\(z_i\)表示第\(i\)类的预测分数。这些分数可以通过softmax函数进行归一化得到预测概率。用q表示softmax运算符q = softmax(z)的输出，i类的概率qi可以通过下式计算：
  $$
  q_i = \frac{exp(z_i)}{\sum_{j=1}^{K} exp(z_j)}
  $$
  这是很容易看出\({q_i > 0}\)，并且\({\sum_{j=1}^{K} q_i = 1}\)，所以q是一个合理的概率分布。

• 对标签设置成one-hot向量形式：假设图像的真实标签为y，则如果i = y，则将真实概率分布构造为pi = 1，否则将其构造为0。在训练期间，通过最小化负交叉熵损失来更新模型参数，以使这两个概率分布彼此相似。特别地，通过p的构造方式，我们知道\(l(p,q) = -logp_y = -z_y + log(\sum_{i=1}^{K} exp(z_i)) \),最佳解决方案是\(z_y^* = \) inf，同时保持其他大小足够小。换句话说，它鼓励显著不同的输出得分，这可能导致过度拟合。

标签平滑

• 起源：标签平滑的思想首先被提出用于训练Inceptionv2。它改变了真实概率的构造为
  $$
  q_i=\begin{cases}
  1-\epsilon,\quad if \quad i=y \\
  \epsilon / (K-1),\quad otherwise,
  \end{cases}
  $$
  其中\(\epsilon\)是一个小常数。